Visualizing The Calculus Of Space: A Deep Dive Into Charts Representing Numerical Integration

Visualizing the Calculus of Space: A Deep Dive into Charts Representing Numerical Integration

Associated Articles: Visualizing the Calculus of Space: A Deep Dive into Charts Representing Numerical Integration

Introduction

With nice pleasure, we are going to discover the intriguing matter associated to Visualizing the Calculus of Space: A Deep Dive into Charts Representing Numerical Integration. Let’s weave fascinating data and provide contemporary views to the readers.

Visualizing the Calculus of Space: A Deep Dive into Charts Representing Numerical Integration

Numerical integration, a cornerstone of utilized arithmetic and scientific computing, tackles the problem of approximating particular integrals when analytical options are unavailable or computationally intractable. Whereas the elemental theorem of calculus offers a sublime theoretical framework, its sensible utility usually necessitates numerical strategies. Understanding these strategies is essential throughout numerous fields, from physics and engineering to finance and information science. This text explores how charts successfully visualize the assorted numerical integration strategies, offering a deeper understanding of their strengths, weaknesses, and sensible implications.

The Essence of Numerical Integration: Approximating Space Below a Curve

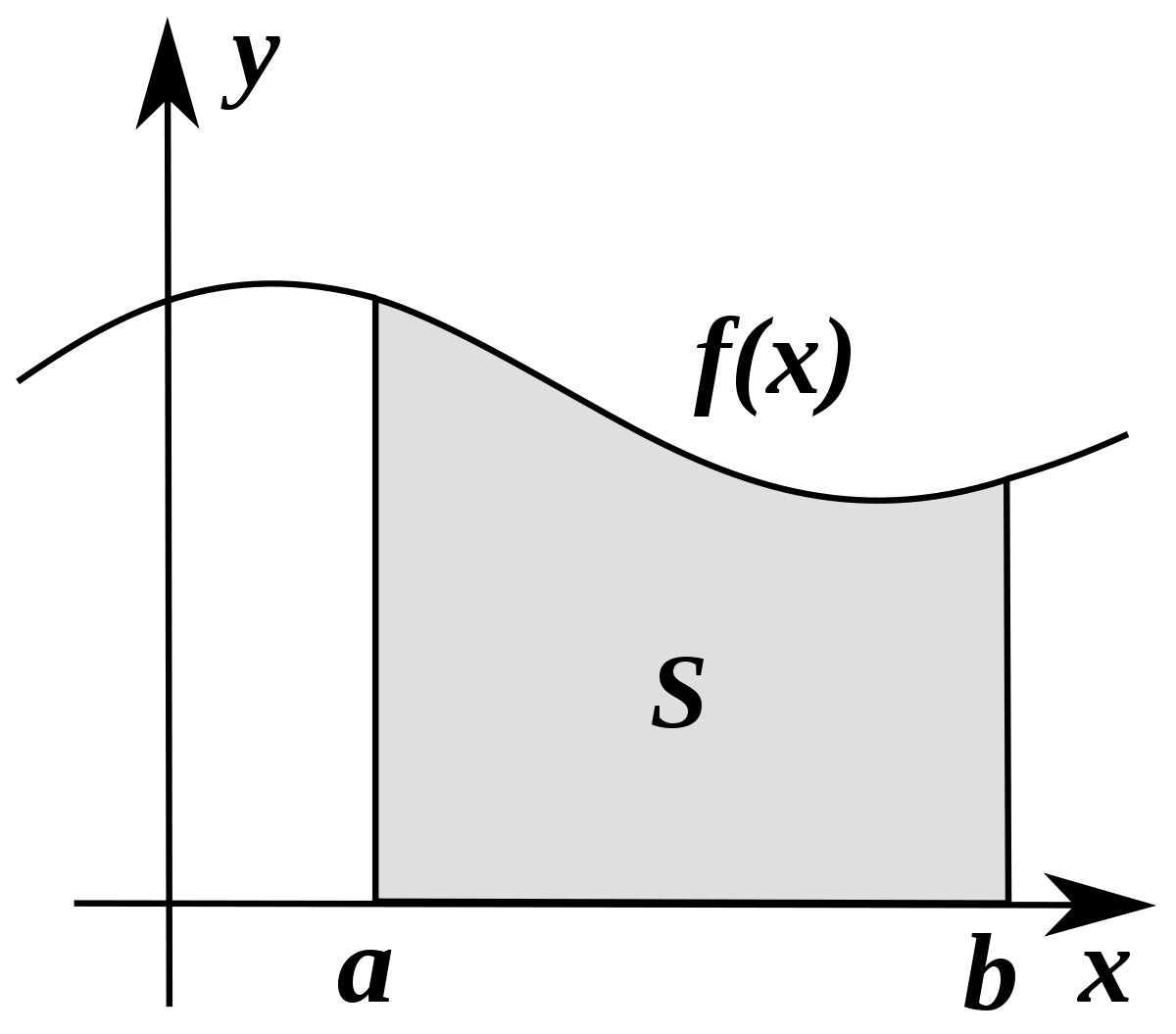
At its core, numerical integration goals to estimate the world underneath a curve outlined by a perform f(x) over a selected interval [a, b]. This space represents the particular integral:

∫_a^b f(x) dx

Analytical integration, utilizing antiderivatives, provides exact options for a lot of capabilities. Nonetheless, many real-world eventualities contain complicated capabilities missing closed-form antiderivatives, necessitating numerical approximations. These approximations partition the combination interval into smaller subintervals and approximate the world inside every subinterval utilizing numerous geometrical shapes. The sum of those approximated areas offers an estimate of the entire space, therefore the integral.

Charting the Strategies: A Visible Exploration

Totally different numerical integration strategies make use of totally different methods for approximating the world underneath the curve. Let’s discover some frequent strategies and visualize them utilizing charts:

1. Rectangular Rule (Midpoint, Left, Proper):

This easiest methodology approximates the world underneath the curve utilizing rectangles. The peak of every rectangle is set by the perform’s worth at a selected level throughout the subinterval.

• Left Rectangular Rule: The peak is the perform’s worth on the left endpoint of every subinterval. A chart would present rectangles whose heights are decided by the perform’s worth on the left edge of every partition, probably underestimating the world if the perform is rising and overestimating if it is lowering.

• Proper Rectangular Rule: The peak is the perform’s worth on the proper endpoint. The chart would mirror the Left Rectangular Rule however utilizing the best edge, resulting in reverse biases in estimation.

• Midpoint Rectangular Rule: The peak is the perform’s worth on the midpoint of every subinterval. This methodology usually provides higher accuracy than the left or proper guidelines, because it mitigates the bias launched by utilizing just one endpoint. The chart would depict rectangles whose heights completely match the perform’s worth on the center of every partition. A visible comparability of those three strategies on a single chart, displaying the rectangles and the true space, would clearly illustrate the variations in approximation.

2. Trapezoidal Rule:

As an alternative of rectangles, the trapezoidal rule makes use of trapezoids to approximate the world. Every trapezoid is fashioned by connecting adjoining factors on the curve with a straight line. This methodology usually offers a extra correct approximation than the oblong rule, particularly for easily various capabilities. A chart would present a collection of trapezoids becoming snugly underneath the curve, illustrating how the linear approximation between factors improves accuracy. A direct comparability chart with the oblong rule would spotlight the improved match of the trapezoids.

3. Simpson’s Rule:

Simpson’s rule makes use of quadratic approximations as a substitute of linear ones (as within the trapezoidal rule). It approximates the world underneath the curve utilizing parabolic segments. This methodology requires an excellent variety of subintervals and usually provides considerably greater accuracy than the oblong or trapezoidal guidelines, notably for easy capabilities. A chart might depict parabolic arcs becoming the curve extra intently than the trapezoids, emphasizing the elevated accuracy. A comparative chart showcasing Simpson’s rule alongside the trapezoidal and rectangular guidelines would vividly display the improved precision.

4. Adaptive Quadrature:

Adaptive quadrature strategies alter the quantity and dimension of subintervals primarily based on the perform’s conduct. They focus extra subintervals in areas the place the perform varies quickly, making certain greater accuracy the place wanted. A chart illustrating adaptive quadrature would present a non-uniform partitioning of the interval, with smaller subintervals in areas of excessive curvature and bigger subintervals in smoother areas. The chart would successfully visualize the strategy’s adaptive nature and its effectivity in dealing with complicated capabilities.

Error Evaluation and Convergence: Visualizing Accuracy

Charts play a vital function in understanding the error related to numerical integration strategies. Error is the distinction between the approximated integral and the true integral. By plotting the error as a perform of the variety of subintervals (or the step dimension), we are able to visually assess the convergence of the strategy. A logarithmic scale for the error axis is commonly used to obviously present the speed of convergence. One of these chart demonstrates how the error decreases because the variety of subintervals will increase, revealing the strategy’s effectivity and its means to realize a desired stage of accuracy.

Comparability Charts: A Highly effective Software for Understanding

Comparative charts are important for evaluating the relative efficiency of various numerical integration strategies. These charts can plot the approximated integral values towards the variety of subintervals for numerous strategies, permitting for a direct visible comparability of their accuracy and effectivity. A well-designed comparability chart will clearly present which methodology converges sooner and achieves greater accuracy with fewer computations.

Past Primary Strategies: Visualizing Superior Methods

Past the essential strategies described above, extra refined strategies exist, reminiscent of Gaussian quadrature and Monte Carlo integration. Visualizing these strategies will be difficult, however charts can nonetheless present helpful insights. For instance, a chart might illustrate the strategically positioned factors utilized in Gaussian quadrature, highlighting the strategy’s effectivity in reaching excessive accuracy with a small variety of perform evaluations.

Conclusion: Charts as Important Instruments in Numerical Integration

Charts are indispensable instruments for understanding and visualizing numerical integration strategies. They supply a strong technique to grasp the underlying ideas, examine totally different strategies, analyze errors, and admire the convergence properties of those essential computational instruments. By visually representing the approximations, charts rework summary mathematical ideas into tangible representations, facilitating a deeper understanding of this important space of utilized arithmetic and its widespread functions throughout numerous scientific and engineering disciplines. The flexibility to interpret and create these charts is a helpful talent for anybody working with numerical strategies and information evaluation. Moreover, the event of interactive charts and visualizations provides even higher potential for exploring and understanding the nuances of numerical integration.

Closure

Thus, we hope this text has offered helpful insights into Visualizing the Calculus of Space: A Deep Dive into Charts Representing Numerical Integration. We thanks for taking the time to learn this text. See you in our subsequent article!