Decoding The Z-Worth Chart: Your Key To Understanding The Regular Distribution

Decoding the Z-Worth Chart: Your Key to Understanding the Regular Distribution

Associated Articles: Decoding the Z-Worth Chart: Your Key to Understanding the Regular Distribution

Introduction

With enthusiasm, let’s navigate by means of the intriguing matter associated to Decoding the Z-Worth Chart: Your Key to Understanding the Regular Distribution. Let’s weave fascinating data and provide contemporary views to the readers.

Decoding the Z-Worth Chart: Your Key to Understanding the Regular Distribution

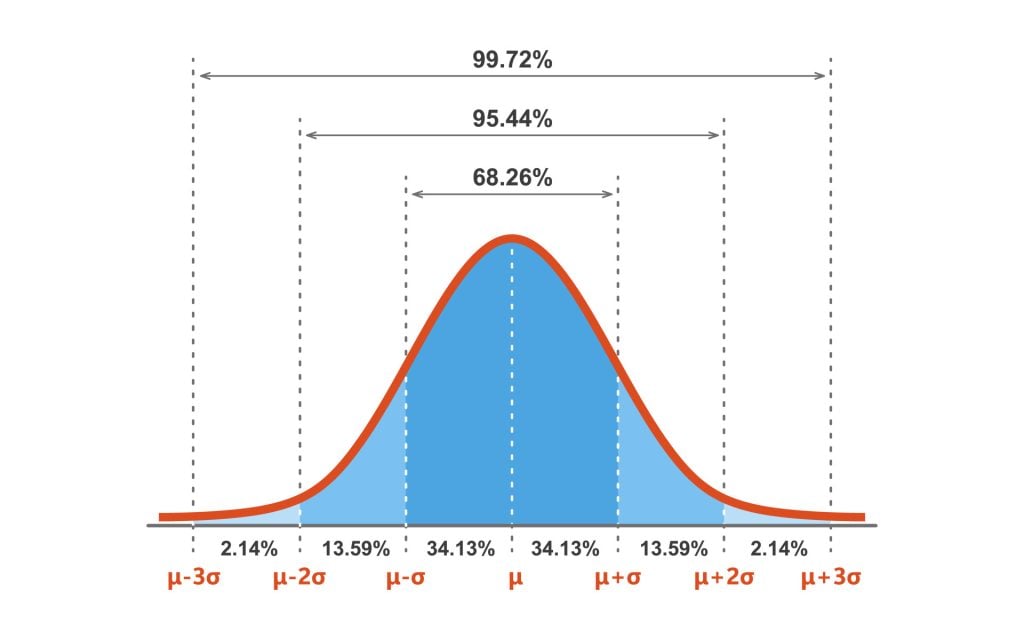
The traditional distribution, usually depicted as a bell curve, is a elementary idea in statistics. It describes the likelihood distribution of a steady random variable, the place the info clusters round a central imply worth, symmetrically really fizzling out in the direction of the extremes. Understanding this distribution is essential throughout quite a few fields, from finance and engineering to drugs and social sciences. A key software in navigating the traditional distribution is the Z-value chart, often known as the usual regular distribution desk. This text will delve into the intricacies of the Z-value chart, explaining its building, utility, and significance in statistical evaluation.

The Basis: Normal Regular Distribution and Z-Scores

Earlier than diving into the chart itself, it is important to understand the idea of the usual regular distribution. It is a particular case of the traditional distribution with a imply (µ) of 0 and a typical deviation (σ) of 1. Any usually distributed variable might be reworked into a typical regular variable utilizing a Z-score. The Z-score represents the variety of commonplace deviations a selected knowledge level lies away from the imply. The formulation for calculating a Z-score is:

Z = (X – µ) / σ

The place:

• Z is the Z-score
• X is the person knowledge level
• µ is the inhabitants imply
• σ is the inhabitants commonplace deviation

The Z-score permits us to standardize knowledge from totally different regular distributions, making them comparable. A optimistic Z-score signifies the info level is above the imply, whereas a detrimental Z-score signifies it is under the imply. A Z-score of 0 means the info level is precisely on the imply.

The Z-Worth Chart: A Desk of Possibilities

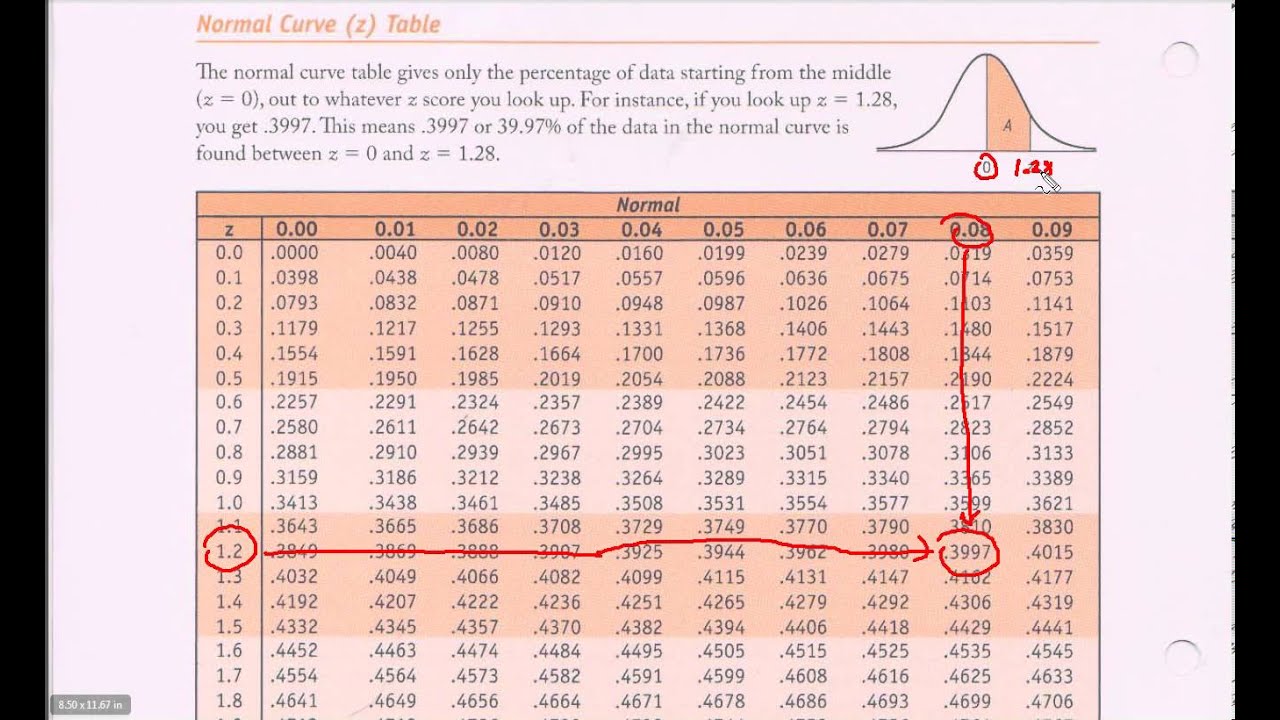
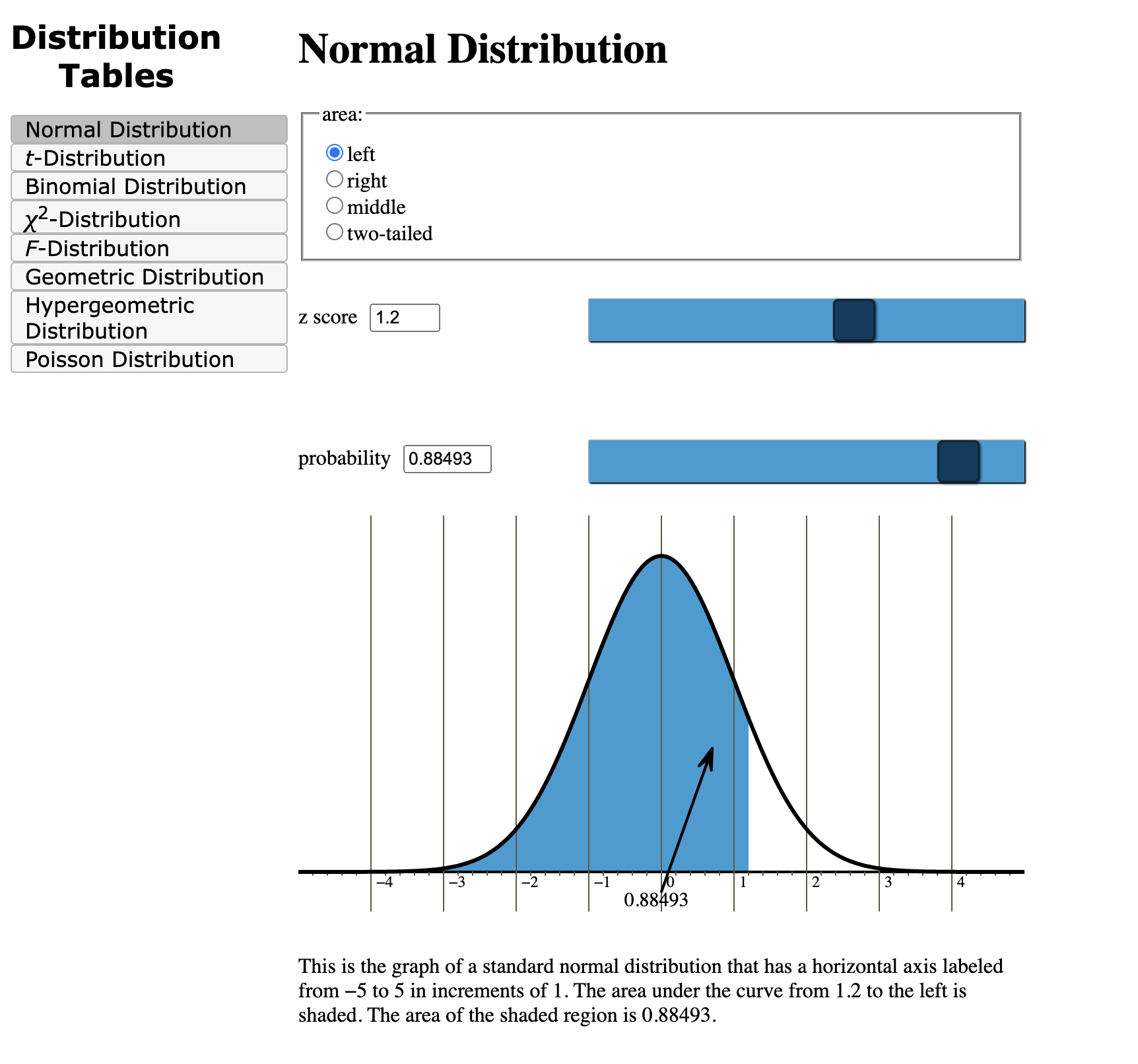
The Z-value chart, or commonplace regular distribution desk, is a tabulation of cumulative possibilities related to totally different Z-scores. It basically offers the likelihood {that a} randomly chosen knowledge level from a typical regular distribution will probably be lower than or equal to a selected Z-score. The chart sometimes presents Z-scores to 2 decimal locations, with the primary decimal place listed within the leftmost column and the second decimal place within the high row. The intersection of the row and column offers the corresponding cumulative likelihood.

For instance, should you search for a Z-score of 1.96, you may discover a likelihood of roughly 0.975. This implies there is a 97.5% probability {that a} randomly chosen knowledge level from a typical regular distribution will probably be lower than or equal to 1.96 commonplace deviations above the imply. Conversely, there is a 2.5% probability will probably be larger than 1.96 commonplace deviations above the imply.

Deciphering the Z-Worth Chart: Key Concerns

A number of essential factors should be thought-about when decoding the Z-value chart:

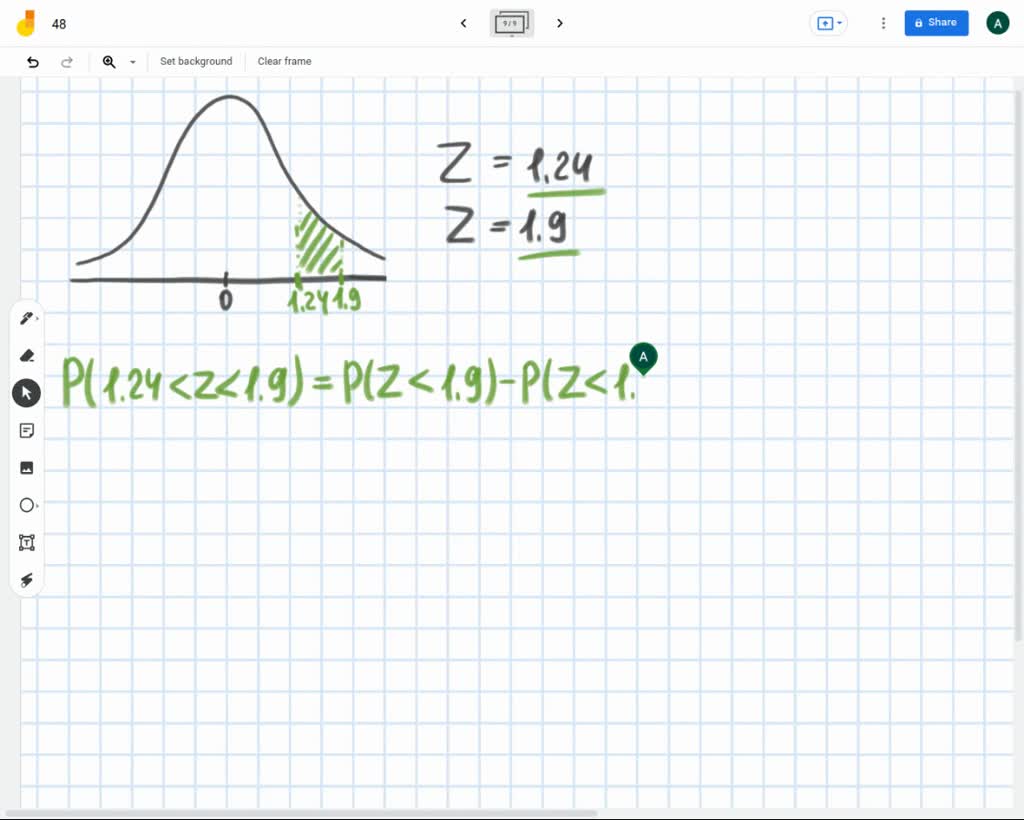
• Cumulative Likelihood: The values within the chart signify cumulative possibilities. They point out the likelihood of observing a worth lower than or equal to the desired Z-score. To seek out the likelihood of observing a worth larger than a given Z-score, subtract the desk worth from 1.

• Symmetry: The usual regular distribution is symmetrical across the imply (0). This implies the likelihood of observing a worth lower than a detrimental Z-score is the same as the likelihood of observing a worth larger than the corresponding optimistic Z-score.

• Space Below the Curve: The possibilities within the Z-value chart correspond to the world beneath the curve of the usual regular distribution. This space represents the proportion of information factors falling inside a selected vary.

• Interpolation: The Z-value chart sometimes offers possibilities for Z-scores to 2 decimal locations. If you have to discover the likelihood for a Z-score with extra decimal locations, you should use interpolation strategies to estimate the worth. Nonetheless, statistical software program packages provide extra exact calculations.

Purposes of the Z-Worth Chart in Statistical Evaluation

The Z-value chart has widespread functions in varied statistical analyses:

• Speculation Testing: Z-tests are used to check hypotheses about inhabitants means when the inhabitants commonplace deviation is understood. The Z-value chart is essential in figuring out the crucial Z-values for rejecting or failing to reject the null speculation at a given significance stage.

• Confidence Intervals: Z-values are used to assemble confidence intervals for inhabitants means. The Z-value chart helps decide the margin of error based mostly on the specified confidence stage.

• Likelihood Calculations: The chart permits for the calculation of possibilities related to particular ranges of values in a usually distributed variable. That is notably helpful in threat evaluation and high quality management.

• Percentile Calculations: The Z-value chart can be utilized to find out the percentile rank of a selected knowledge level inside a usually distributed dataset. For instance, discovering the Z-score similar to the ninety fifth percentile permits one to find out the worth above which 95% of the info lies.

• Information Standardization and Comparability: As talked about earlier, Z-scores permit for the standardization of information from totally different regular distributions. This allows significant comparisons between datasets with totally different means and commonplace deviations.

Limitations of the Z-Worth Chart

Whereas the Z-value chart is a robust software, it has sure limitations:

• Assumption of Normality: The chart’s applicability depends on the belief that the info follows a standard distribution. If the info is considerably non-normal, utilizing the Z-value chart can result in inaccurate conclusions. Assessments for normality, such because the Shapiro-Wilk check, needs to be carried out earlier than making use of the Z-value chart.

• Precision: The chart sometimes offers possibilities to just a few decimal locations. For greater precision, statistical software program is beneficial.

• Pattern Measurement: The Z-value chart is most correct when coping with giant pattern sizes. For small pattern sizes, the t-distribution may be extra acceptable.

Past the Z-Worth Chart: Using Statistical Software program

Whereas the Z-value chart offers a invaluable understanding of the traditional distribution and its possibilities, fashionable statistical software program packages provide much more environment friendly and exact strategies for calculating possibilities and performing associated analyses. Software program like R, SPSS, SAS, and Python’s SciPy library present features that immediately calculate Z-scores, possibilities, and confidence intervals, eliminating the necessity for guide lookups and interpolation. These instruments additionally provide extra superior strategies for dealing with non-normal knowledge and small pattern sizes.

Conclusion

The Z-value chart is a elementary software for understanding and dealing with the traditional distribution. Its skill to translate uncooked knowledge into standardized Z-scores and supply related possibilities makes it invaluable in speculation testing, confidence interval building, and varied different statistical analyses. Nonetheless, it is essential to recollect its limitations, notably the belief of normality and the necessity for big pattern sizes. Whereas the chart offers a invaluable conceptual understanding, using statistical software program for extra exact and environment friendly calculations is strongly beneficial for real-world functions. Mastering the Z-value chart, coupled with the utilization of statistical software program, offers a strong basis for tackling a variety of statistical issues throughout numerous disciplines.

Closure

Thus, we hope this text has offered invaluable insights into Decoding the Z-Worth Chart: Your Key to Understanding the Regular Distribution. We hope you discover this text informative and helpful. See you in our subsequent article!