Decoding The Z-Rating Desk: A Complete Information

Decoding the Z-Rating Desk: A Complete Information

Associated Articles: Decoding the Z-Rating Desk: A Complete Information

Introduction

With enthusiasm, let’s navigate via the intriguing matter associated to Decoding the Z-Rating Desk: A Complete Information. Let’s weave attention-grabbing data and provide recent views to the readers.

Decoding the Z-Rating Desk: A Complete Information

The z-score desk, often known as the usual regular distribution desk, is a vital instrument in statistics. It is a cornerstone for understanding chances related to usually distributed knowledge. This desk gives the cumulative likelihood (space underneath the curve) for a given z-score, representing the likelihood {that a} randomly chosen worth from a normal regular distribution might be lower than or equal to that z-score. This text will delve deep into the z-score desk, explaining its development, interpretation, and varied functions, accompanied by illustrative examples.

Understanding Z-Scores and the Normal Regular Distribution:

Earlier than we dive into the intricacies of the z-score desk, let’s refresh our understanding of z-scores and the usual regular distribution. A z-score represents the variety of customary deviations a knowledge level is away from the imply of a distribution. The method for calculating a z-score is:

z = (x – μ) / σ

The place:

• x is the person knowledge level.
• μ is the inhabitants imply.
• σ is the inhabitants customary deviation.

A normal regular distribution is a traditional distribution with a imply (μ) of 0 and a normal deviation (σ) of 1. Remodeling uncooked knowledge into z-scores permits us to standardize the information, making it simpler to check values from totally different distributions and to make use of the z-score desk for likelihood calculations.

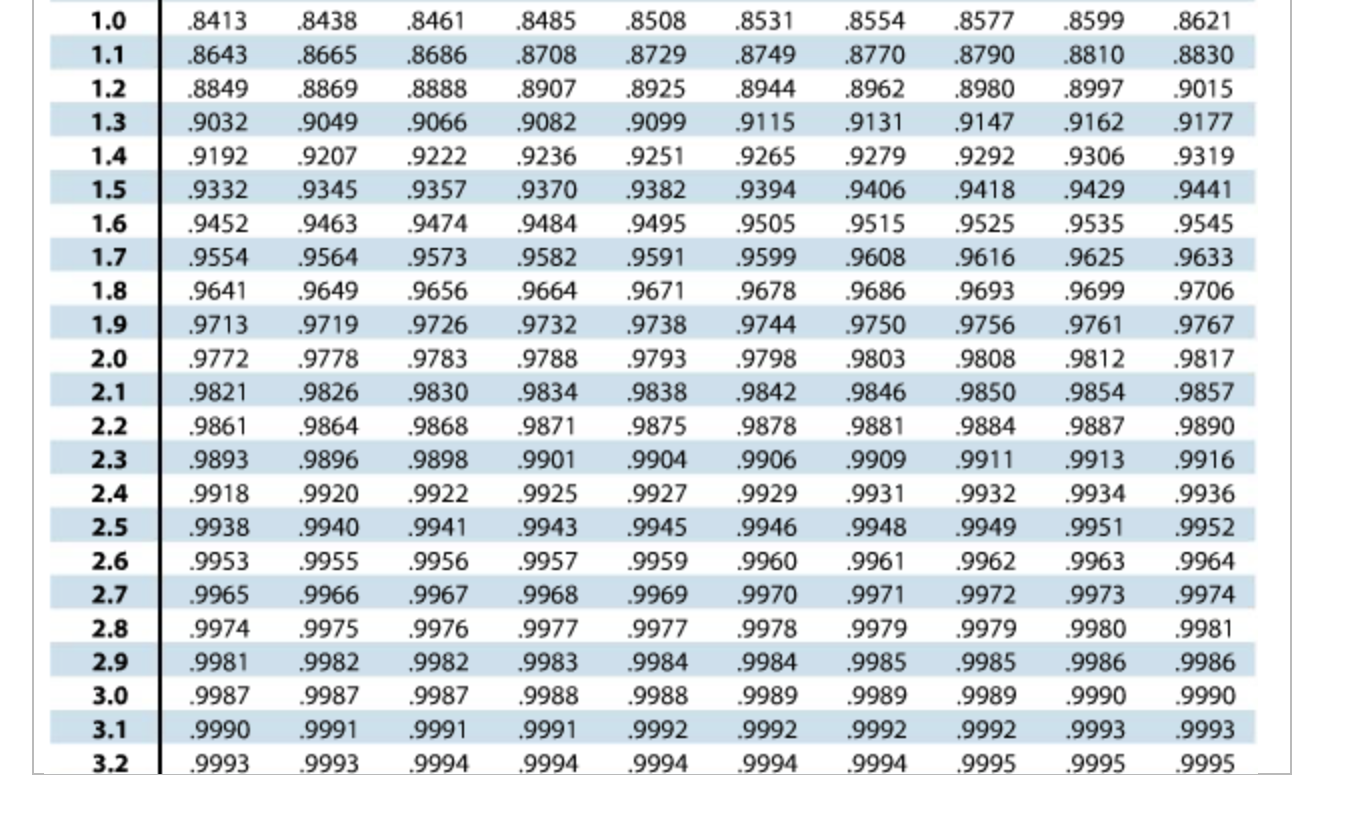
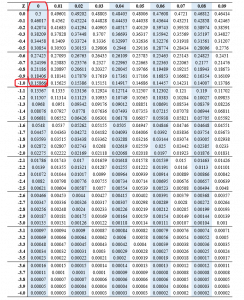
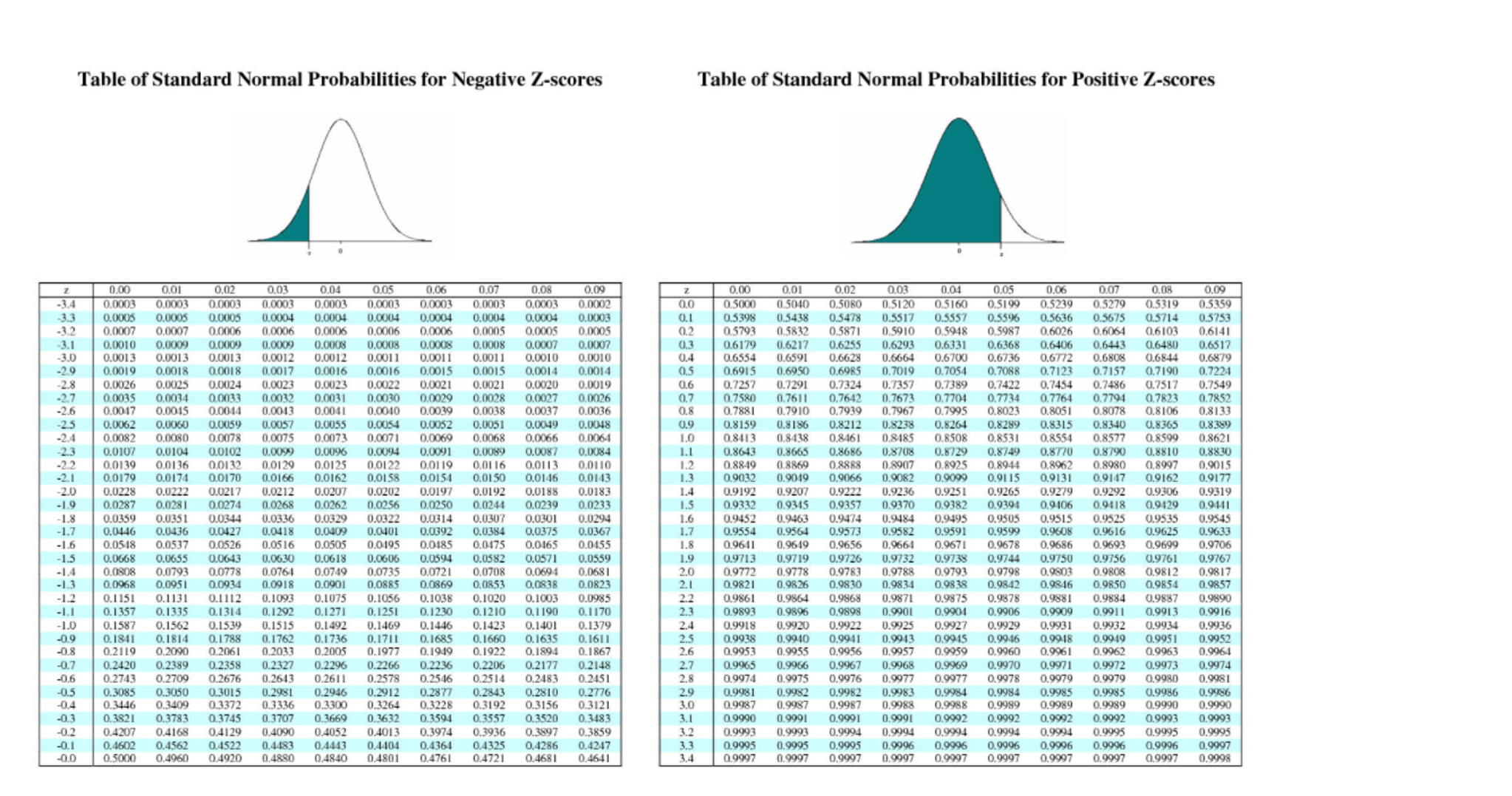
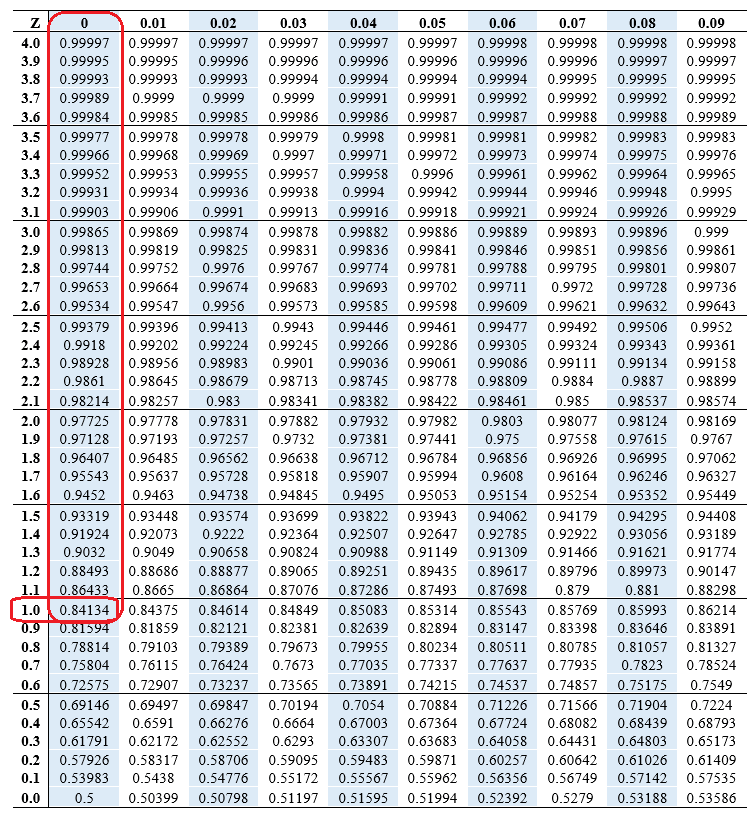
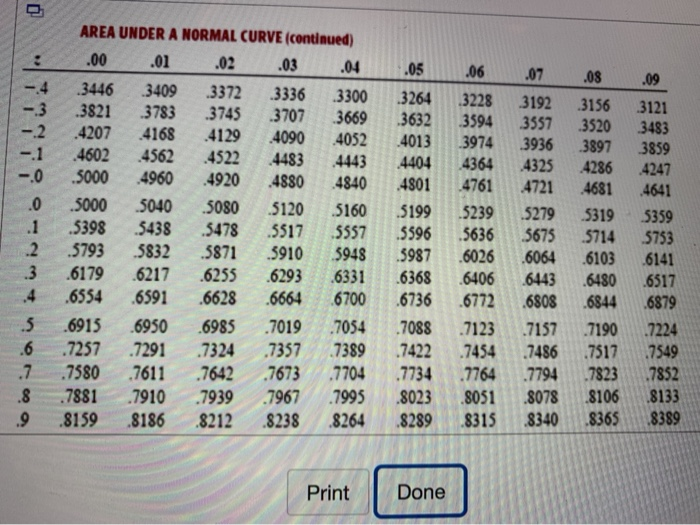
Construction and Interpretation of the Z-Rating Desk:

The z-score desk sometimes presents the cumulative likelihood, typically denoted as P(Z ≤ z), for a given z-score. The desk is often organized as follows:

• Rows signify the entire quantity and tenths place of the z-score. For instance, the row for z = 1.2 would signify z-scores between 1.20 and 1.29.
• Columns signify the hundredths place of the z-score. These columns sometimes vary from 0.00 to 0.09.
• The intersection of a row and a column provides the cumulative likelihood. This likelihood represents the world underneath the usual regular curve to the left of the required z-score.

As an illustration, should you lookup z = 1.23 within the desk, you will discover a worth comparable to the likelihood of a z-score being lower than or equal to 1.23. This worth represents the world underneath the curve to the left of 1.23.

Instance utilizing the Z-Rating Desk:

For instance we need to discover the likelihood {that a} randomly chosen worth from a normal regular distribution is lower than or equal to 1.58.

1. Find the row comparable to 1.5.
2. Find the column comparable to 0.08.
3. Discover the intersection of the row and column. This worth would be the cumulative likelihood.

The worth on the intersection will sometimes be round 0.9429. This implies there is a 94.29% likelihood {that a} randomly chosen worth from a normal regular distribution might be lower than or equal to 1.58.

Calculating Possibilities for Completely different Situations:

The z-score desk gives the cumulative likelihood to the left of the z-score. Nevertheless, we frequently must calculate chances for various eventualities:

• Chance of Z being larger than a worth: P(Z > z) = 1 – P(Z ≤ z). Subtract the desk worth from 1.
• Chance of Z being between two values: P(z1 < Z < z2) = P(Z ≤ z2) – P(Z ≤ z1). Subtract the cumulative likelihood of the decrease z-score from the cumulative likelihood of the upper z-score.
• Discovering a z-score given a likelihood: This requires utilizing the desk in reverse. Discover the likelihood closest to the given likelihood within the desk’s physique after which establish the corresponding z-score.

Purposes of the Z-Rating Desk:

The z-score desk has wide-ranging functions throughout varied fields:

• Speculation Testing: Z-tests make the most of the z-score desk to find out the p-value, which helps in making choices about rejecting or failing to reject a null speculation.
• Confidence Intervals: The z-score desk is essential in calculating confidence intervals for inhabitants means and proportions. The suitable z-score is used to find out the margin of error.
• High quality Management: In manufacturing and different industries, z-scores are used to observe course of variation and establish outliers.
• Finance: Z-scores are utilized in threat administration and portfolio evaluation to evaluate the likelihood of utmost occasions.
• Medication: Z-scores are used to standardize medical check outcomes and examine them to a reference inhabitants.
• Training: Z-scores can be utilized to check pupil efficiency throughout totally different colleges or courses.

Limitations of the Z-Rating Desk:

Whereas the z-score desk is a strong instrument, it has sure limitations:

• Accuracy: The desk gives approximate values. Extra exact calculations require statistical software program.
• Assumption of Normality: The z-score desk is just relevant when the information is often distributed or roughly usually distributed. For non-normal knowledge, different strategies are wanted.
• Pattern Dimension: For small pattern sizes, the z-test might not be applicable, and different exams, such because the t-test, ought to be used.

Past the Primary Desk: Utilizing Know-how for Z-Rating Calculations:

Whereas the z-score desk is a priceless studying instrument, statistical software program packages like R, SPSS, Python (with libraries like SciPy), and Excel provide extra exact and environment friendly methods to calculate chances and z-scores. These instruments can deal with extra complicated eventualities and supply larger accuracy than a printed desk. They’ll additionally calculate chances for z-scores past the vary sometimes lined in a normal desk.

Conclusion:

The z-score desk is an indispensable instrument for understanding and dealing with usually distributed knowledge. Its capacity to transform uncooked scores into standardized z-scores and supply corresponding chances is crucial for varied statistical analyses. Whereas the desk itself gives a priceless understanding of the underlying ideas, fashionable statistical software program provides extra exact and versatile alternate options for sensible functions. Mastering using the z-score desk, nonetheless, stays a foundational ability for anybody working with statistical knowledge. Understanding its construction, interpretation, and limitations is essential for correct and significant statistical evaluation.

Closure

Thus, we hope this text has supplied priceless insights into Decoding the Z-Rating Desk: A Complete Information. We admire your consideration to our article. See you in our subsequent article!