Decoding The T-Distribution Chart: A Complete Information

Decoding the t-Distribution Chart: A Complete Information

Associated Articles: Decoding the t-Distribution Chart: A Complete Information

Introduction

On this auspicious event, we’re delighted to delve into the intriguing subject associated to Decoding the t-Distribution Chart: A Complete Information. Let’s weave fascinating info and supply contemporary views to the readers.

Decoding the t-Distribution Chart: A Complete Information

The t-distribution, a cornerstone of inferential statistics, performs a vital function in speculation testing and confidence interval estimation when coping with small pattern sizes or unknown inhabitants commonplace deviations. In contrast to the traditional distribution, which depends on realizing the inhabitants parameters, the t-distribution accounts for the uncertainty launched by estimating these parameters from pattern information. This text delves into the intricacies of the t-distribution chart, exploring its properties, purposes, and how one can interpret its values successfully.

Understanding the t-Distribution

The t-distribution, also called Scholar’s t-distribution (because of its authentic publication below the pseudonym "Scholar"), is a household of likelihood distributions characterised by a single parameter: the levels of freedom (df). The levels of freedom characterize the variety of impartial items of data out there to estimate the inhabitants variance. Within the context of a t-test, the levels of freedom are usually calculated as n – 1, the place n is the pattern measurement.

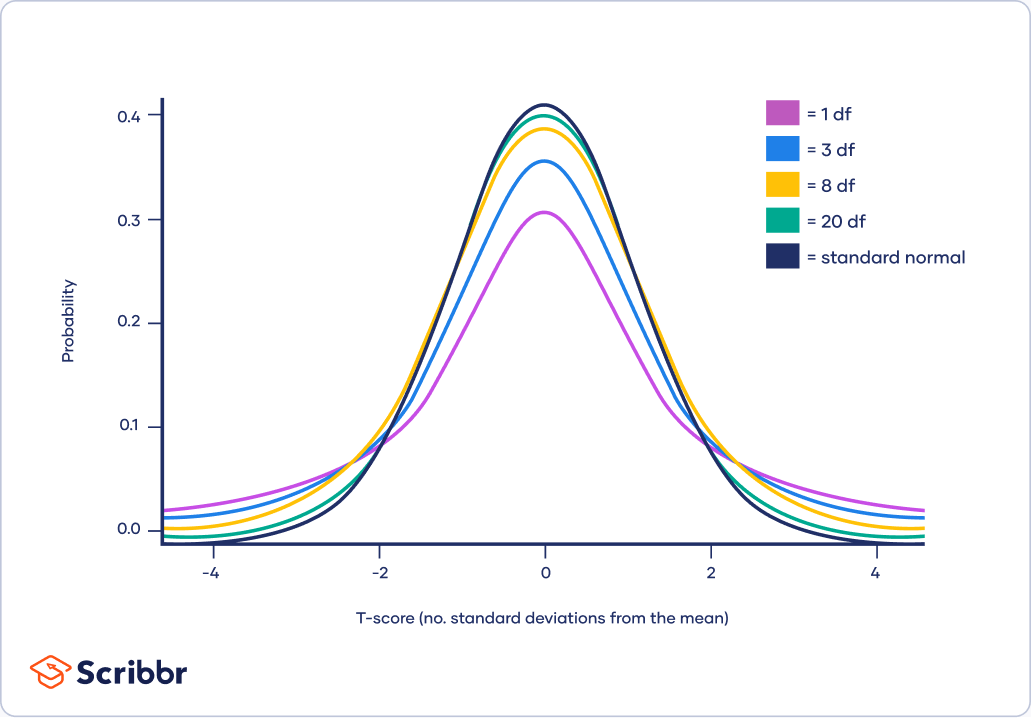
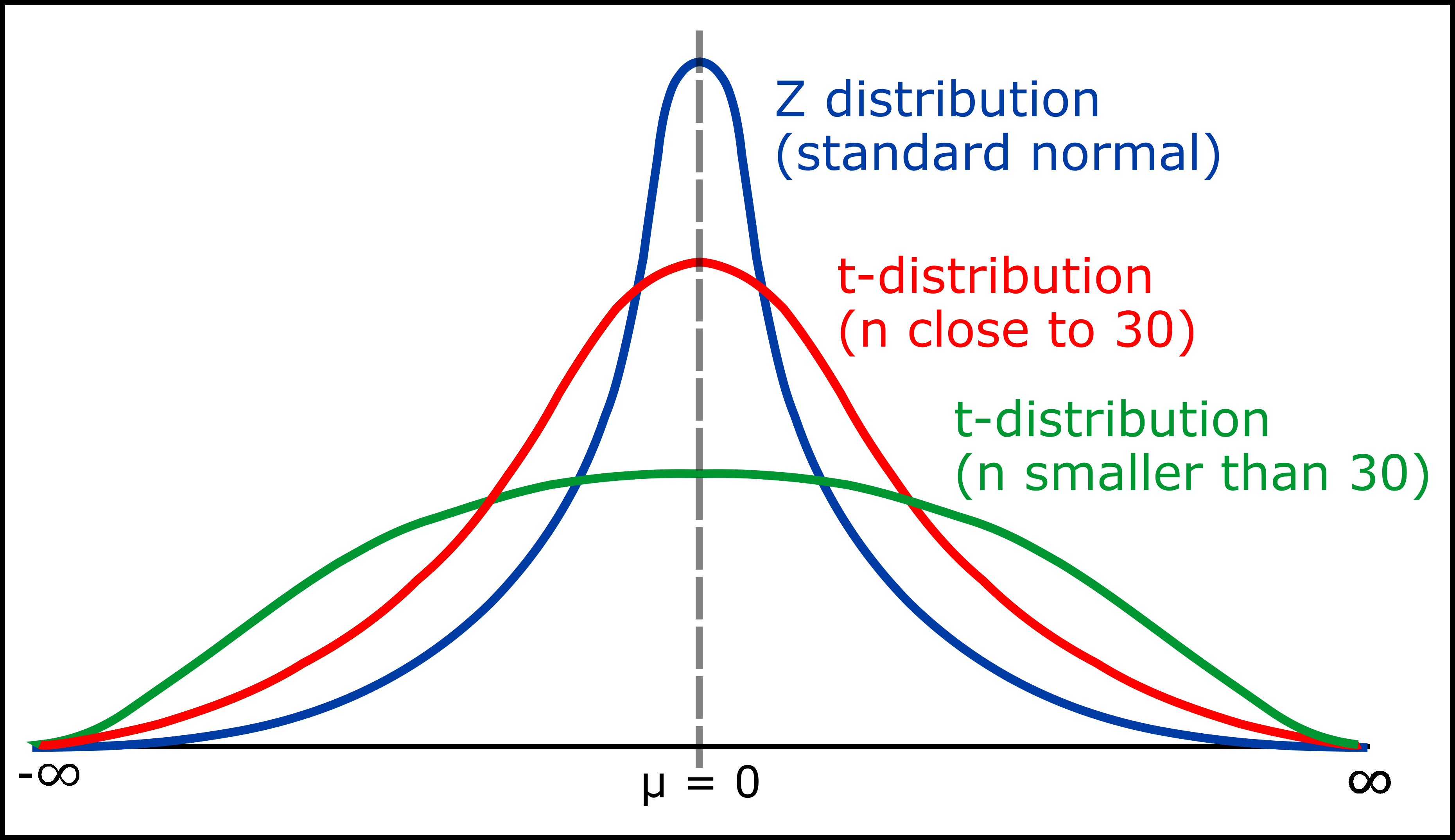
In contrast to the traditional distribution, which is bell-shaped and symmetrical round its imply (0), the t-distribution can also be bell-shaped and symmetrical, however its tails are heavier. Because of this the t-distribution has a larger likelihood of observing excessive values in comparison with the traditional distribution. Because the levels of freedom enhance, the t-distribution progressively approaches the traditional distribution. With a big sufficient pattern measurement (usually thought-about to be above 30), the distinction between the t-distribution and the traditional distribution turns into negligible.

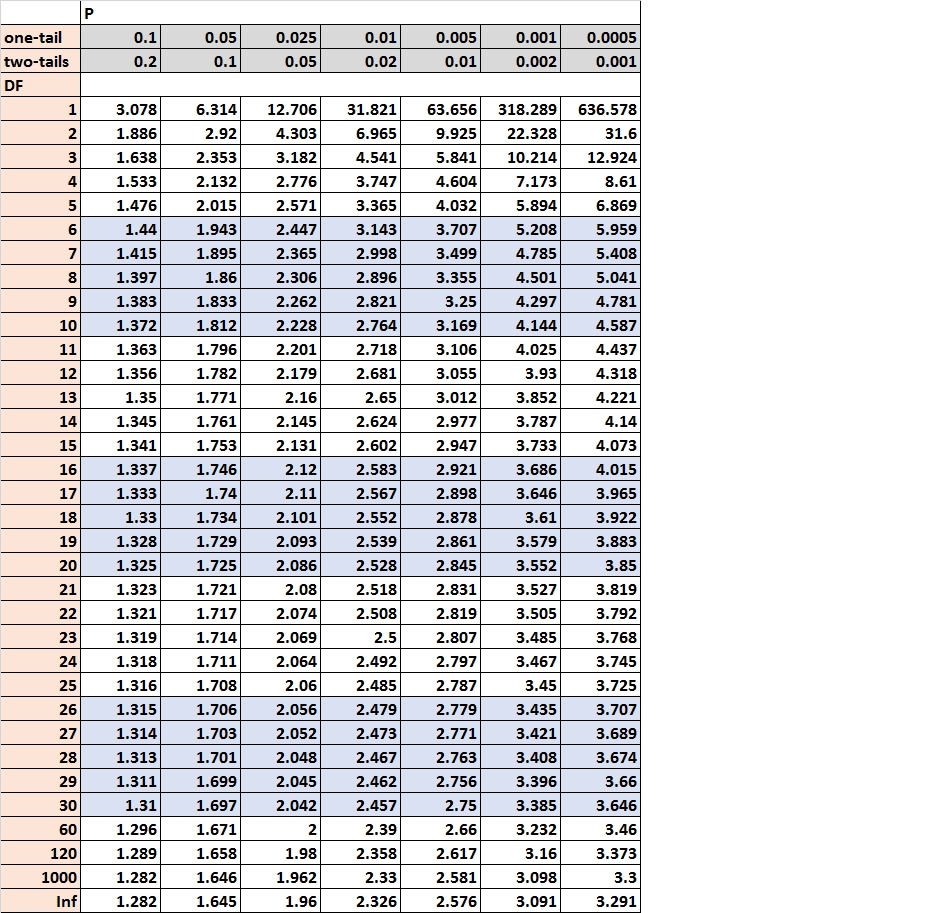
The t-Distribution Chart (Desk): Construction and Interpretation

The t-distribution chart, usually introduced as a desk, gives vital values of the t-distribution for various ranges of significance (alpha) and levels of freedom. These vital values outline the boundaries of the rejection area in a speculation check. The desk usually follows this construction:

• Rows: Signify the levels of freedom (df). These values usually vary from 1 to infinity (or a big quantity representing a near-normal distribution).
• Columns: Signify the alpha stage (significance stage) or the corresponding confidence stage (1 – alpha). Widespread alpha ranges embody 0.10, 0.05, 0.025, 0.01, and 0.005. These characterize the likelihood of rejecting the null speculation when it’s really true (Sort I error). The corresponding confidence ranges are 90%, 95%, 97.5%, 99%, and 99.5%, respectively.
• Cell Values: The intersection of a row (df) and a column (alpha) provides the vital t-value. That is the worth that the calculated t-statistic should exceed (in absolute worth) to reject the null speculation on the specified alpha stage.

Instance of a t-Distribution Desk Entry:

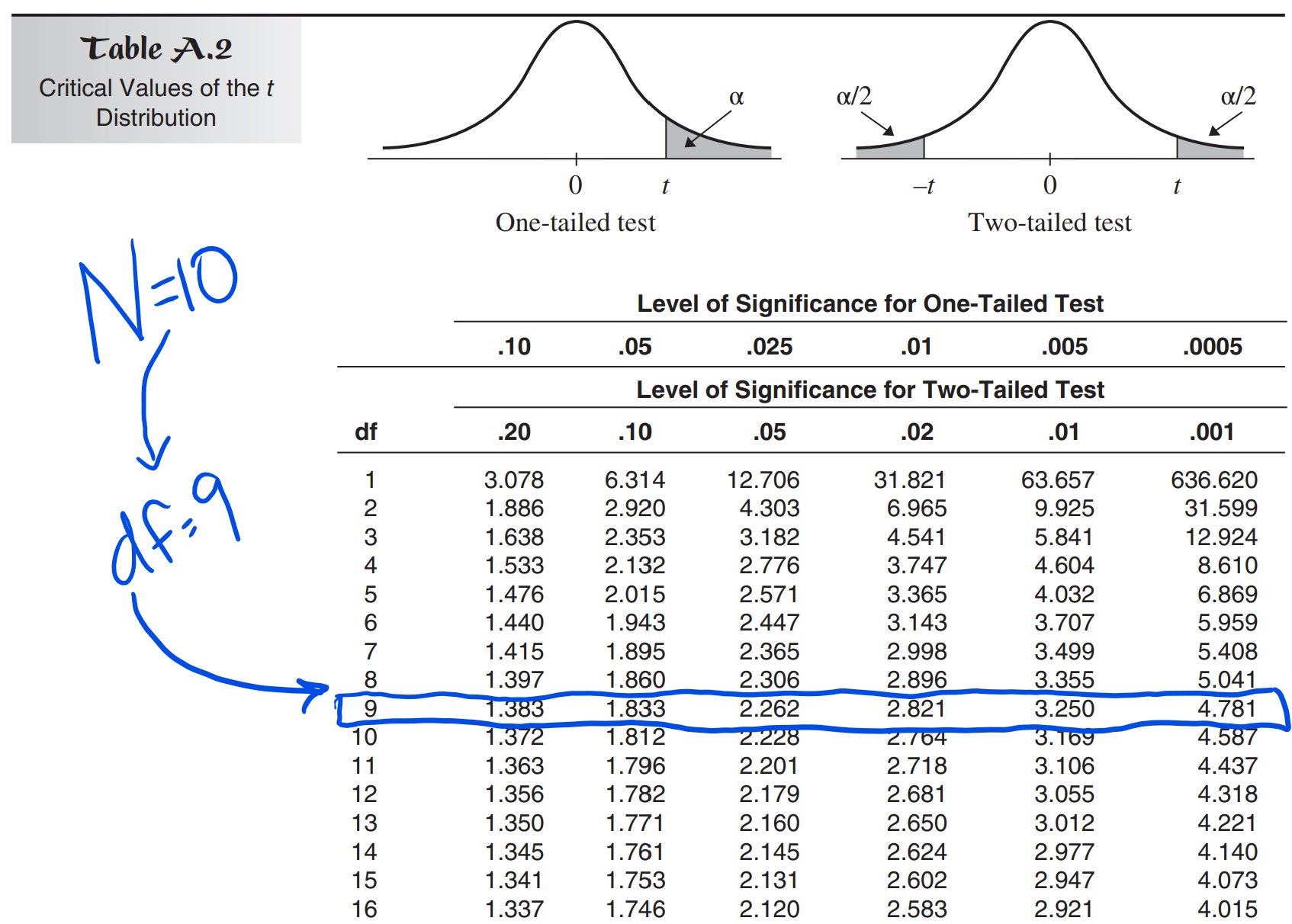
For instance you might have a desk entry that exhibits a worth of two.131 on the intersection of df = 10 and alpha = 0.05 (two-tailed check). Because of this in case you are conducting a two-tailed t-test with 10 levels of freedom and a significance stage of 0.05, you’d reject the null speculation in case your calculated t-statistic is lower than -2.131 or larger than 2.131.

One-Tailed vs. Two-Tailed Exams:

The t-distribution chart can be utilized for each one-tailed and two-tailed checks.

• Two-tailed check: This checks whether or not the inhabitants imply is considerably completely different from a hypothesized worth in both path (larger than or lower than). On this case, the alpha stage is split by 2 (e.g., 0.05 turns into 0.025), and the vital t-value is discovered on the intersection of the chosen df and the adjusted alpha stage. The rejection area is cut up into two tails of the distribution.

• One-tailed check: This checks whether or not the inhabitants imply is considerably completely different from a hypothesized worth in a selected path (both larger than or lower than). On this case, the alpha stage is used instantly, and the vital t-value is discovered on the intersection of the chosen df and the alpha stage. The rejection area is situated in just one tail of the distribution.

Functions of the t-Distribution Chart:

The t-distribution chart is instrumental in varied statistical procedures:

• One-sample t-test: Compares the imply of a single pattern to a recognized or hypothesized inhabitants imply.
• Two-sample t-test (impartial samples): Compares the technique of two impartial teams to find out if there is a important distinction between them.
• Paired t-test: Compares the technique of two associated teams (e.g., before-and-after measurements on the identical topics).
• Confidence interval estimation: Calculates a spread of values inside which the true inhabitants imply is prone to fall with a specified stage of confidence. The t-distribution is used to find out the margin of error within the confidence interval calculation. The components usually entails the vital t-value obtained from the chart.

Deciphering Outcomes Utilizing the t-Distribution Chart:

The method of utilizing the t-distribution chart usually entails these steps:

1. State the hypotheses: Outline the null and different hypotheses.
2. Decide the importance stage (alpha): Select the specified stage of significance (e.g., 0.05).
3. Calculate the levels of freedom (df): That is based mostly on the pattern measurement and the precise check being carried out.
4. Calculate the t-statistic: This entails calculating the distinction between the pattern imply and the hypothesized inhabitants imply, and dividing by the usual error of the imply.
5. Discover the vital t-value: Find the vital t-value within the t-distribution chart utilizing the calculated levels of freedom and the chosen alpha stage (contemplating whether or not it is a one-tailed or two-tailed check).
6. Evaluate the calculated t-statistic to the vital t-value:
   • If absolutely the worth of the calculated t-statistic is larger than the vital t-value, reject the null speculation.
   • If absolutely the worth of the calculated t-statistic is lower than or equal to the vital t-value, fail to reject the null speculation.

Limitations of the t-Distribution Chart:

Whereas the t-distribution chart is a robust software, it has sure limitations:

• Assumption of normality: The t-test assumes that the information is roughly usually distributed. If the information considerably deviates from normality, particularly with small pattern sizes, the outcomes of the t-test could also be unreliable. Non-parametric checks must be thought-about in such instances.
• Homogeneity of variance (for two-sample t-tests): For impartial samples t-tests, the idea of equal variances within the two teams is essential. If this assumption is violated, different checks like Welch’s t-test must be used.
• Small pattern sizes: Whereas the t-distribution is designed for small pattern sizes, extraordinarily small pattern sizes (e.g., n < 5) can nonetheless result in unreliable outcomes.

Technological Developments and the t-Distribution:

Immediately, statistical software program packages (like R, SPSS, SAS, and Python’s SciPy library) have rendered the guide use of t-distribution charts largely out of date. These applications present exact t-values and p-values (the likelihood of acquiring outcomes as excessive as, or extra excessive than, the noticed outcomes, assuming the null speculation is true) instantly, eliminating the necessity for guide desk lookups. Nevertheless, understanding the underlying ideas of the t-distribution and its chart stays essential for decoding the output of those software program packages and for greedy the basic ideas of statistical inference.

Conclusion:

The t-distribution chart is a helpful software for conducting speculation checks and establishing confidence intervals when coping with small pattern sizes or unknown inhabitants variances. Whereas trendy statistical software program automates the method, understanding the construction and interpretation of the t-distribution chart is important for comprehending the core ideas of statistical inference and for critically evaluating statistical outcomes. By mastering the ideas introduced on this article, researchers and analysts can confidently make the most of the t-distribution to attract significant conclusions from their information.

Closure

Thus, we hope this text has offered helpful insights into Decoding the t-Distribution Chart: A Complete Information. We thanks for taking the time to learn this text. See you in our subsequent article!